Capire un cifrario Simmetrico ( AES )

Cos’è un cifrario simmetrico#

Un cifrario simmetrico è un particolare algoritmo di cifratura in cui la chiave utilizzata per cifrare il testo in chiaro (plaintext) è la stessa chiave utilizzata per decifrare il testo cifrato (ciphertext).

Scopo :

• rendere un messaggio decifrabile solo per chi ha una particolare chiave (key)

Vantaggio principale :

• è un algoritmo estremamente rapido e veloce se ho la chiave, impiego poco tempo per cifrare/decifrare un messaggio

Svantaggio principale:

• come posso passare la chiave in maniera affidabile ad un’altra persona ?

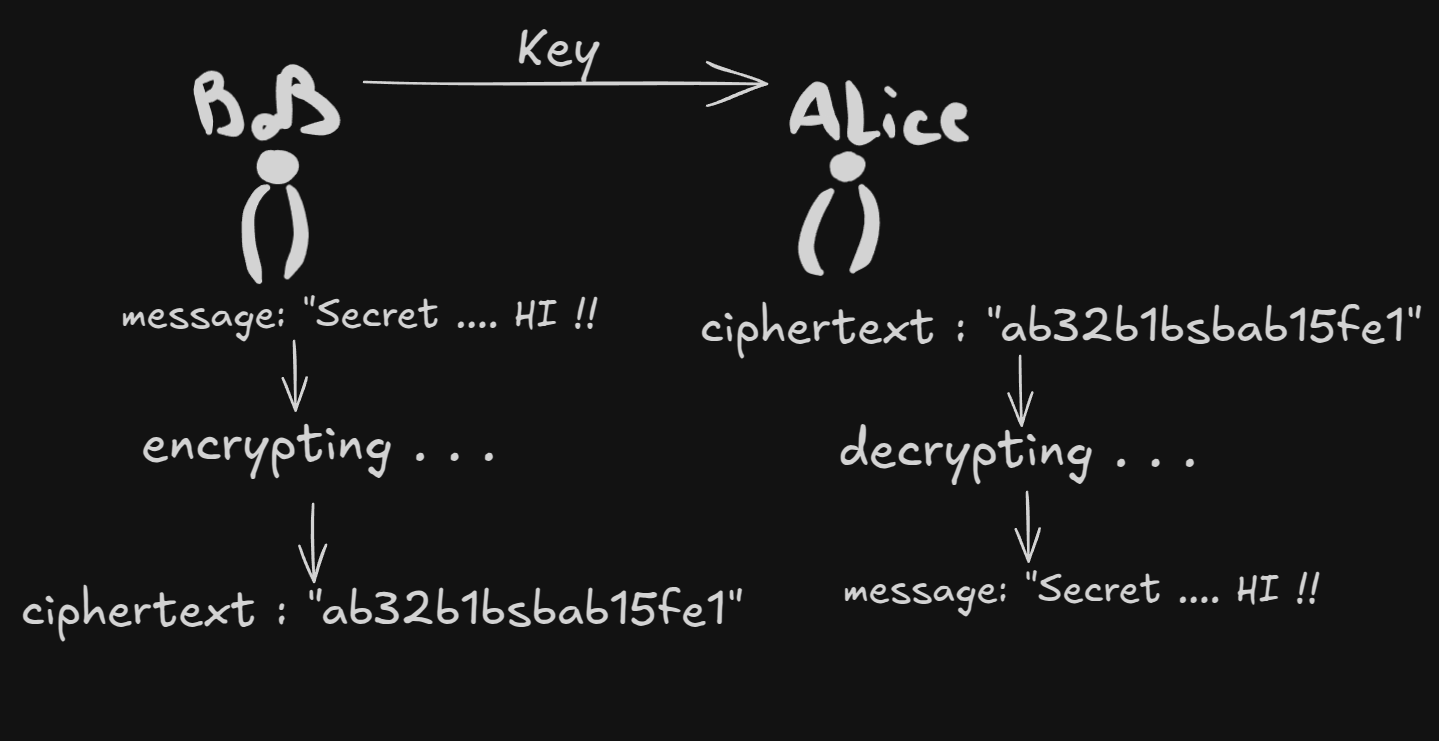
Come funziona sotto la scocca (AES)#

Discuteremo del funzionamento del cifrario simmetrico AES (Advanced Encryption Standard) in quanto standard concreto in molte applicazioni reali … Senza saperlo, lo usiamo tutti noi, ogni giorno, quando ci connettiamo in rete ( certificato TLS/SSL ) !!

L’algoritmo lavora su blocchi di lunghezza fissa di 16 Byte (16 caratteri, utilizzando ASCII), su cui applica diversi round di cifratura utilizzando i byte della chiave (anche la lunghezza della chiave deve essere divisibile per blocchi di 16 Byte)

Ogni round consiste nel :

• AddRoundKey : lo stato attuale (partendo dal plaintext, al primo round) viene XORato con la key fornita
• SubBytes : i byte dello stato vengono sostituiti con altri byte (non-linear substitution) secondo una particolare lookup table
• Shift: step in cui vengono mischiati le righe con le colonne (transposizione matriciale)

Ciò che si ottiene alla fine dei round è un testo cifrato della stessa lunghezza del testo in chiaro fornito (divisibili in blocchi da 16 Byte)

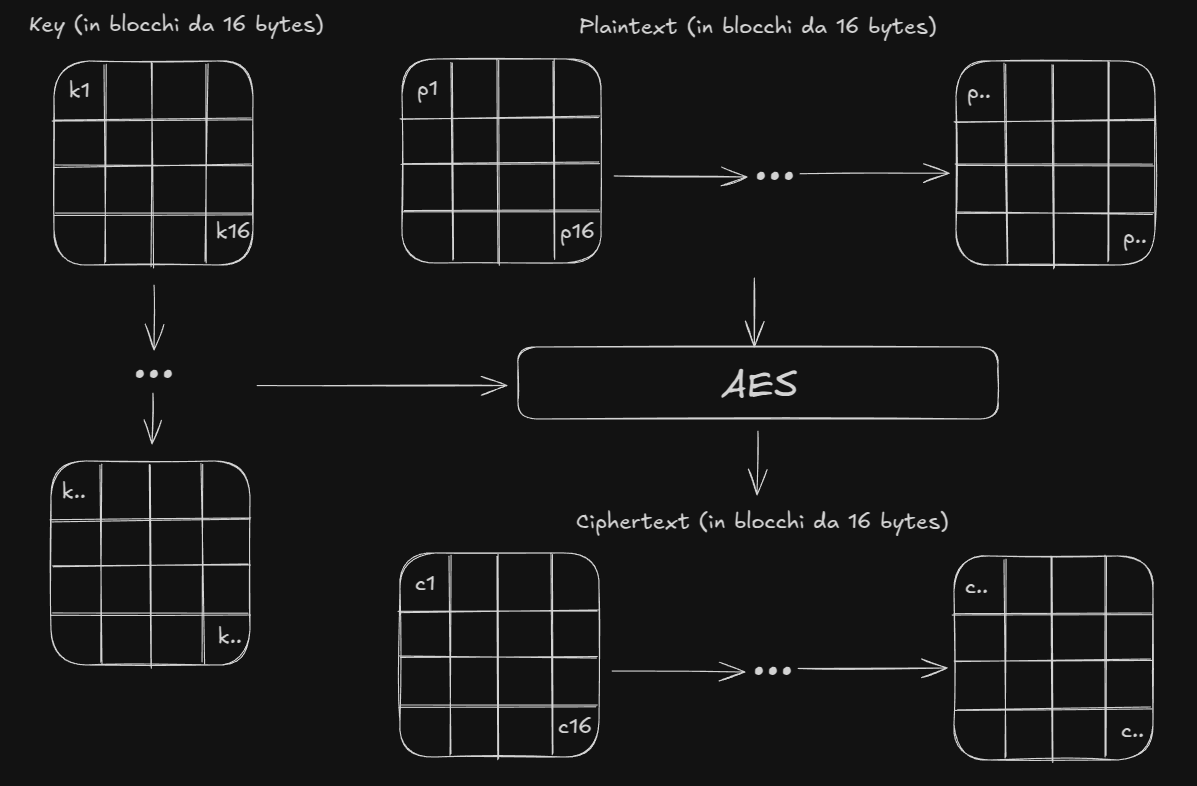
Un dubbio lecito sulla lunghezza di plaintext, key e ciphertext#

Abbiamo appena detto che tutto ciò che viene dato in pasto all’AES deve essere divisibile in blocchi da 16 bytes … ciò vuol dire che possiamo cifrare solamente testi divisibili per 16 caratteri, utilizzando solamente chiavi lunghe 16 caratteri ?! Teoricamente si ! Nella pratica … ovviamente NO ! fortunatamente esiste il PADDING

Padding#

Per risolvere il problema dei blocchi di grandezza fissa, nelle applicazioni pratiche di AES viene utilizzato il padding, ossia una funzione (più o meno complessa) per ottenere stringhe di lunghezza divisibile per 16, partendo da stringhe di lunghezza generica

la funzione più utilizzata (PKCS#7)#

È una funzione di padding molto semplice che aggiunge N bytes mancanti, di valore N, alla stringa di lunghezza generica, per arrivare ad un multiplo di 16

Esempio pratico …

• stringa di lunghezza generica : “CIAO BOB!” lunghezza -> 9 bytes (CIAO -> 4 bytes + spazio -> 1 byte + BOB! -> 4 bytes)

• N valore -> 7 (16 - 9, sono i bytes mancanti alla stringa per essere divisibile in blocchi da 16)

• stringa + padding -> “CIAO BOB!07070707070707” (sono stati aggiunti N bytes di valore N, ossia 7 byte di valore 7, se ci sono dubbi su questo, ripassare la tabella ASCII e come funzionano le conversioni carattere -> byte)

Esempio in python …

from Crypto.Util.Padding import pad

stringa = b'Ciao BOB!'
block_size = 16 # AES block size

padded_data = pad(stringa, block_size, style='pkcs7')

# padded_data -> b'Ciao BOB!\x07\x07\x07\x07\x07\x07\x07'

Per far girare il codice in locale ti servirà pycryptodome (libreria fondamentale), usare un Virtual Environment è caldamente consigliato

pip install pycryptodome

Cifrare qualcosa … nella PRATICA (in python)#

Ora passiamo alla pratica, cifrando qualche messaggio con python (utilizzando anche la libreria pycryptodome!)

from Crypto.Cipher import AES
import binascii
from Crypto.Util.Padding import pad

BLOCK_SIZE = 16
key = b'Chiave segreta!!'
msg = (b'Ciao BOB!')

padded_plaintext = pad(msg, BLOCK_SIZE, style='pkcs7')
cipher1 = AES.new(key, AES.MODE_CBC)
cipher2 = AES.new(key, AES.MODE_CBC)

msg_en1 = cipher1.encrypt(padded_plaintext)
msg_en2 = cipher2.encrypt(padded_plaintext)

# msg_en1 = b'8de9b6c0acdfe565566a09e0cd4a950a' print(binascii.hexlify(msg_en1))
# msg_en2 = b'1639315063e2405eeca77b0ad46a141d' print(binascii.hexlify(msg_en2))

Se ottieni questo errore (o qualcosa di simile … ricordati di fare il padding del plaintext!)

    raise ValueError("Data must be aligned to block boundary in ECB mode")
ValueError: Data must be aligned to block boundary in ECB mode

Bene … abbiamo cifrato il nostro plaintext ed abbiamo printato a schermo i bytes cifrati relativi al ciphertext … ma … alcuni dubbi

• AES.new(key, AES.MODE_CBC) inizializza un oggetto cifrario utilizzabile una sola volta (per cifrare o decifrare, per motivi di sicurezza
• Perchè nell’inizializzazione dell’oggetto cifrario è presenta la specifica AES.MODE_CBC ? Questo perchè l’algoritmo AES è affiancato da una modalità, ossia una logica di gestione dei blocchi (vedere sotto per ulteriori specifiche)
• Perchè nonostante abbiamo cifrato lo stesso plaintext con la stessa chiave, abbiamo ottenuto due ciphertext differenti ? Questo è dovuto alla presenza dell’Initialization Vector (IV) (vedere sotto), che in generale garantisce, a parità di plaintext e chiave, dei risultati diversi -> questo è interessante perchè in generale siamo interessati a proprietà simili in grandi applicazioni

Modalità nell’AES (mode_cbc, mode_ecb ecc…)#

Ipotizziamo di voler gestire i blocchi nella maniera più semplice possibile, ossia la modalità ECB La logica è la seguente … SENZA UTILIZZARE IV, prendiamo ogni blocco del plaintext, lo cifriamo utilizzando la chiave AES, e riportiamo il blocco cifrato direttamente come blocco che costituirà il ciphertext Schema : MODALITÀ ECB

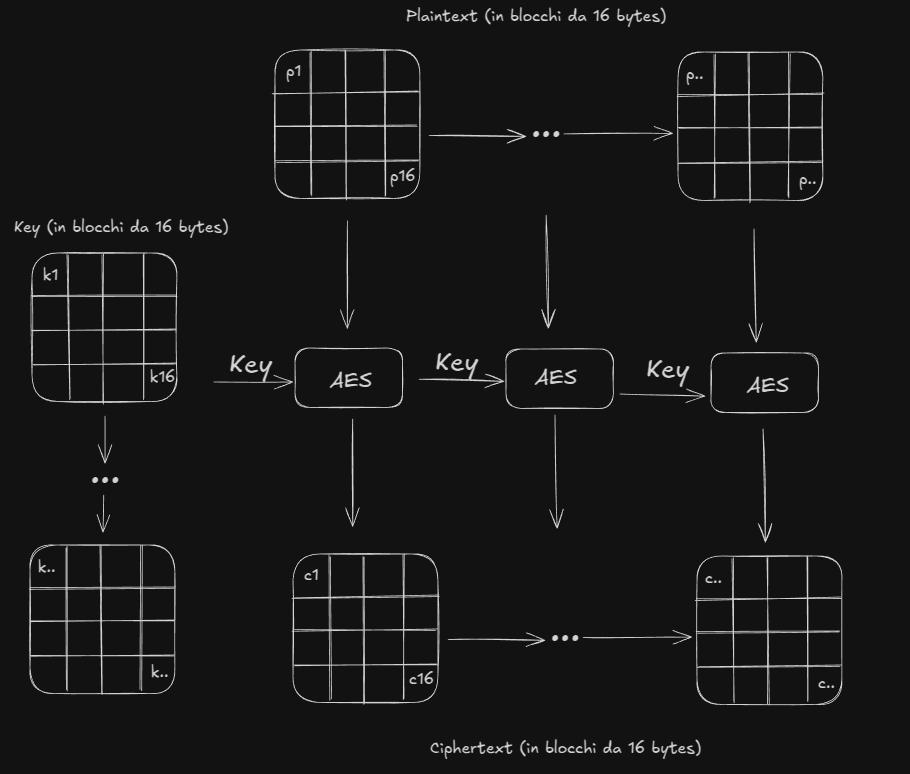
Perchè un approccio così semplice può essere pericoloso#

Ipotizziamo di avere un oracolo che :#

• cifra una stringa generica che noi gli diamo in pasto, appendendola alla fine di una stringa segreta -> encrypt(stringa generica + stringa segreta)
• utilizza una chiave fissa per cifrare le stringhe
• ha una stringa segreta, cifrata, che dobbiamo scoprire
• utilizza la modalità ECB senza IV

Approccio da evitare :#

• supponiamo di avere la stringa segreta da decifrare di lunghezza 32 bytes (con padding)
• NON FUNZIONA cercare di brute-forzare blocco per blocco (16 bytes alla volta) … troppe possibilità (precisamente caratteri possibili elevato alla 16 … quindi circa 40^16 = 1.23 * 10^24 !!)

Approccio vincente :#

• cerchiamo di manipolare i blocchi cifrati così da brute-forzare un singolo carattere alla volta, facendo leva sulla conoscenza della logica con cui viene aggiunto il padding

Capire la lunghezza della stringa da decifrare#

Per capire la lunghezza della stringa segreta da decrifrare, ci basta:

• vedere quanti blocchi è lunga la stringa cifrata, se non aggiungiamo caratteri (se per esempio è lunga 32 bytes allora la lunghezza sarà compresa tra 16 e 31 caratteri NB. se fosse stata lungha 32 bytes, il padding avrebbe aggiunto un intero blocco fatto da 16 0x16 bytes)
• sappiamo quindi che la stringa è composta da un blocco sicuramente completo (da 16 bytes) e da un’altro blocco con del padding
• Per capire quanto è lungo il blocco incompleto ci basta aggiungere alla stringa vuota (che torna 2 blocchi), dei caratteri a caso, e vedere per quale numero preciso di caratteri casuali il cifrato ha un nuovo blocco !
• Quel nuovo blocco sarà un blocco cifrato con solo solo caratteri di padding ! !

Se non inseriamo nulla#

l’oracolo ritorna quindi cypher(""+stringa segreta)

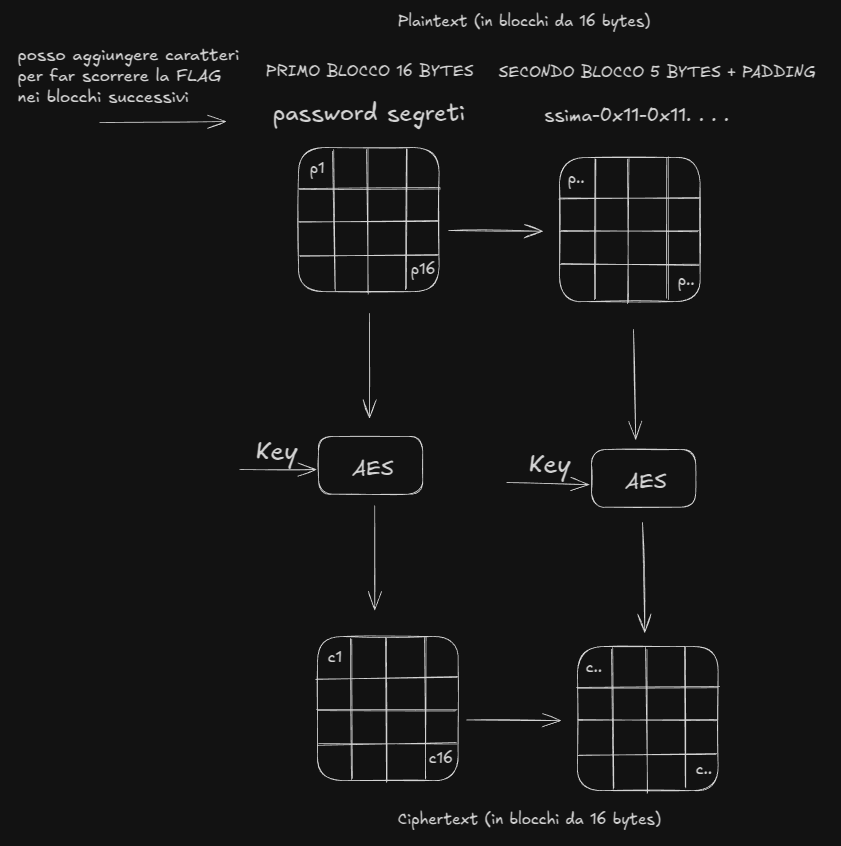
Se inseriamo alcuni caratteri#

l’oracolo ritorna cypher(“CC”+ stringa segreta), abbiamo comportato uno scorrimento di alcuni caratteri della stringa segreta

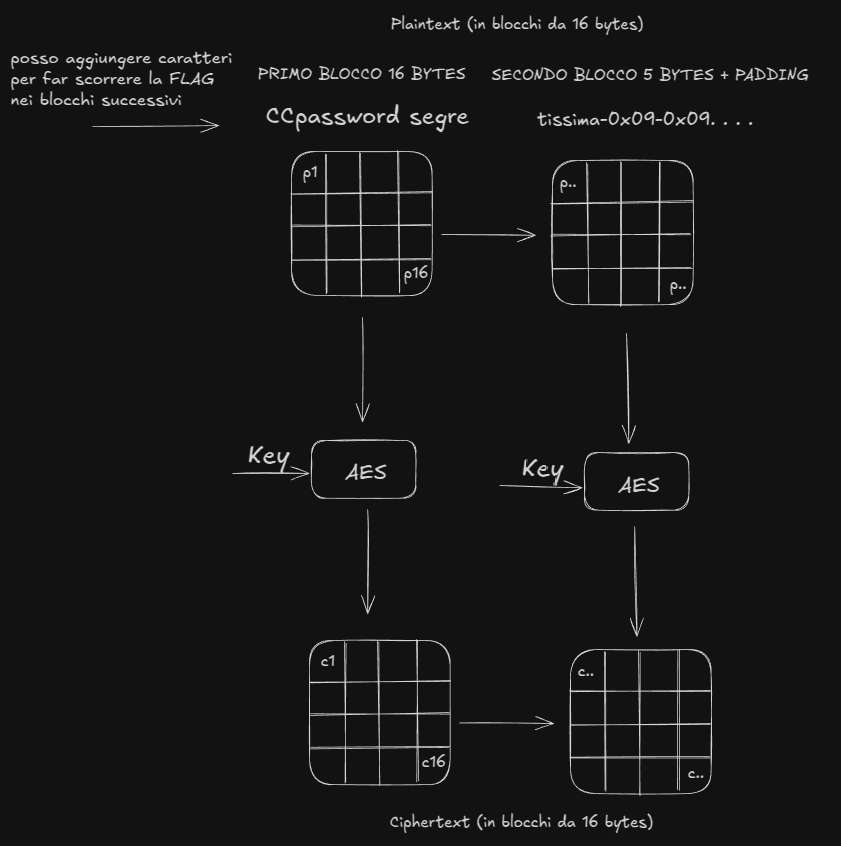
Se inseriamo caratteri fino ad ottenere un nuovo blocco#

l’oracolo ritorna cypher(“CCCCCCCCCCC”+stringa segreta+BLOCCO DI PADDING), il blocco di padding viene generato in quanto la stringa è perfettamente multipla di 32

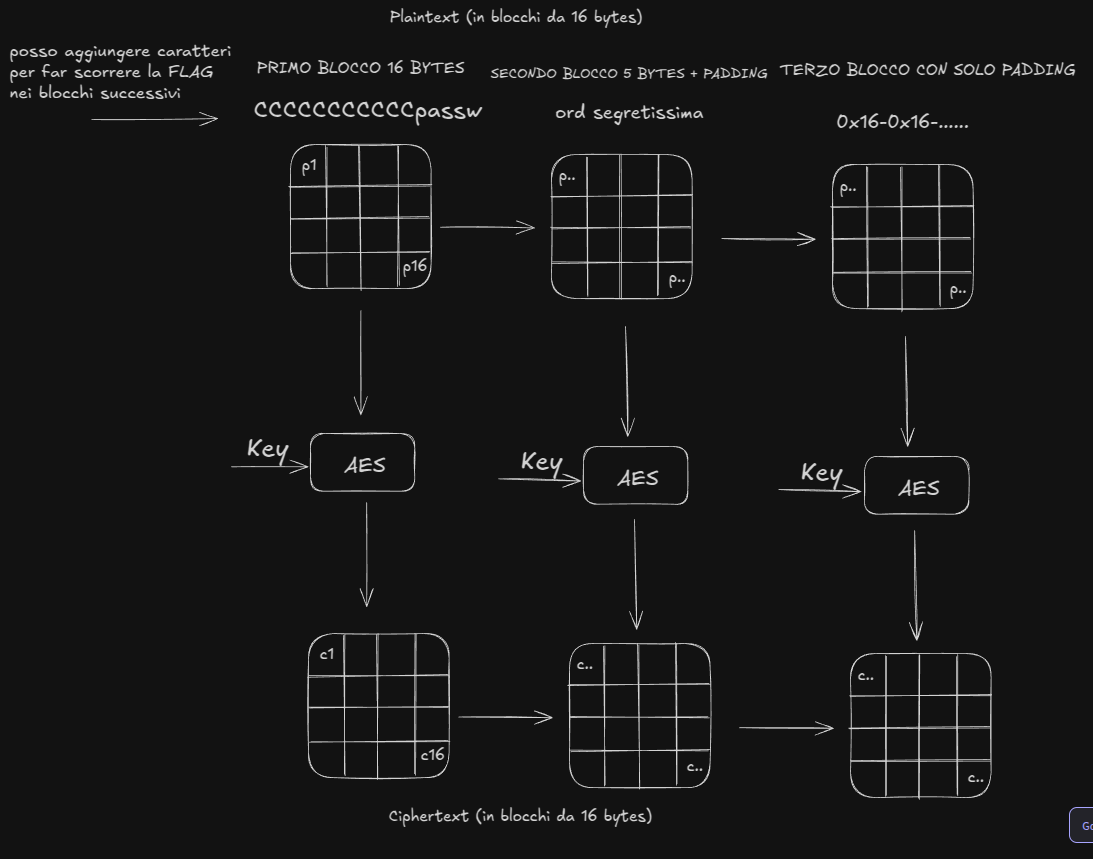
Ora che sappiamo la lunghezza della stringa segreta (32 - numero di caratteri a caso inviati per far generare un nuovo blocco) -> 32-11 = 21 (che infatti è la lunghezza della stringa password segretissima), possiamo iniziare a brute-forzare carattere per carattere, continuando ad inserire caratteri casuali e facendo scorrere ogni carattere della stringa segreta

Brute-force carattere per carattere#

Continuando ad inserire la 12esima ‘C’, avremo questa situazione

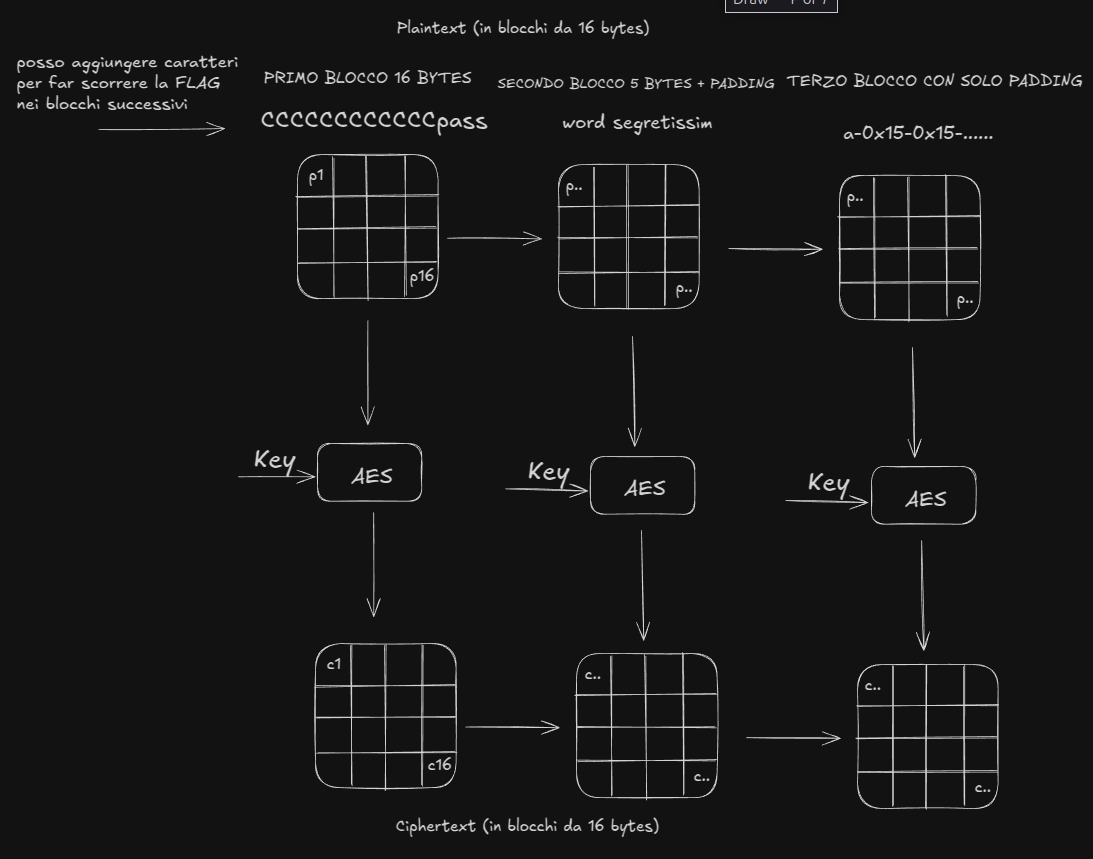
L’ultimo blocco sarà costituito solamente dalla prima lettera della stringa segreta -> “a” più 15 caratteri, che conosciamo, di padding

Possiamo quindi chiedere all’oracolo, giocando sempre con padding e lunghezza della nostra stringa generica, di cifrare, tra i vari blocchi, un blocco appositamente costruito così :

carattere_generico = 'p' # faremo variare questo carattere tra tutti i possibili
blocco_bruteforce = carattere_generico + ( b'0x15'*15)

Ci basta solo chiedere all’oracolo di cifrare il blocco bruteforce, e analizzando il primo blocco ottenuto da cypher(blocco_bruteforce+stringa segreta) e confrontandolo con il terzo blocco ottenuto da cypher(‘CCCCCCCCCCC’+stringa segreta) otterremo il primo carattere della stringa segreta

Da qui in poi la soluzione per trovare l’intera stringa segreta è banale e viene lasciata al lettore :D

Un approccio più rapido#

Invece di mandare blocco per blocco, possiamo mandare tutti gli N blocchi contenenti gli N caratteri brute-forzati in una sola richiesta !! Otterremo così la scoperta di un nuovo carattere della stringa segreta ad ogni nuova richiesta (nel precedente approccio avremmo dovuto fare circa 40 richieste per ogni carattere)

Una modalità più sicura, CBC#

Abbiamo analizzato e compreso le grosse vulnerabilità della modalità ECB … nonostante l’impenetrabilità di AES, gestendo in maniera poco accurata i blocchi, si rischia di ottenere un sistema insicuro

Analizziamo ora la gestione dei blocchi nella modalità CBC:

FONTE : https://ctf101.org/cryptography/what-are-block-ciphers/

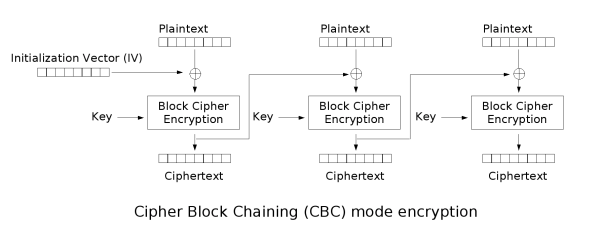
In questa modalità abbiamo bisogno anche di un IV, che viene XORato con il primo blocco di plaintext, PRIMA di essere cifrato con AES I successivi blocchi di plaintext, verrano XORati con i precedenti blocchi di ciphertext, prima di essere cifrati con AES

Perchè è più sicura di ECB#

la modalità CBC è più robusta e sicura di ECB per diversi motivi:

• presenza di un IV casuale, che rende a parità di chiave utilizzata, ogni cifratura diversa
• presenza degli XOR tra i blocchi, che rende ogni blocco strettamente dipendente dai precedenti, rendendo più complesso l’attacco

Vulnerabilità della modalità CBC#

nonostante sia più sicuro di ECB, anche CBC è attaccabile, in presenza di particolari vulnerabilità

In particolare :

• se l’IV è compromesso e si conosce una versione cifrata della stessa stringa, con diverso IV, si possono ottenere, svolgerendo XOR a ritroso, versioni valide di quella stringa cifrata, utilizzando l’IV compromesso
• se l’IV è manipolabile e l’attaccante può scegliere come manipolare l’IV, si possono ricevere rischiosi attacchi di bit-flipping